The superheavy atom is proposed to collapse when the atomic number (Z) exceeds a certain value, which is a fundamental problem of quantum electrodynamics. However, this intriguing supercritical collapse phenomenon remains elusive in experiments because it is almost impossible for natural atoms to satisfy the supercritical condition (Zα>1, α∼1/137 is the fine structure constant). In 2018, Jian Wang group and collaborators discovered log-periodic quantum oscillations in magnetoresistance of topological material ZrTe5 (Science Advances 4, eaau5096 (2018)), revealing the quasi-bound states formed by massless Dirac fermions and opposite charges through strong Coulomb attraction. These quasi-bound states are in the supercritical regime and can be considered as artificial superheavy atoms, which establishes the topological material as a new platform for studying supercritical atomic collapse states.
The discovery of log-periodic quantum oscillations suggests that the supercritical quasi-bound states in Dirac materials shows a novel property of discrete scale invariance (DSI) or discrete scale symmetry. DSI is a scale anomaly with the violation of the continuous scale symmetry, characterized by intriguing log-periodicity. In classical physical systems, DSI exists in fractal structures. In quantum systems, DSI requires that the Hamiltonian of the system satisfies both scale invariance and quantization. The breaking of continuous scale symmetry to discrete scale symmetry is a paradigm of quantum phase transition, which plays an important role in some fundamental quantum systems, such as Schrodinger system with an attractive inverse square (1/r2) potential, (2+1)-dimensional quantum electrodynamics and Efimov effect in cold atom systems. Therefore, the investigation of DSI is important for understanding the underlying physics of nature. However, experimental investigation of DSI in many-body systems such as condensed matter materials is highly challenging.
The local density of states (DOS) near the atomic charged impurities can be directly detected by scanning tunneling microscopy (STM) experiments and the atomic collapse states in graphene have been reported in previous STM studies. However, only two quasi-bound states are reported in graphene systems and thus the characteristic of log-periodicity cannot be fully demonstrated. Therefore, unambiguous evidence of the DSI property of the atomic collapse states is still highly desired. Since 2018, Jian Wang group has reported the log-periodic quantum oscillation involving five oscillating cycles in topological materials ZrTe5, HfTe5 and ZrTe5 (HfTe5) flakes (Science Advances 4, eaau5096 (2018), National Science Review, 6, 914 (2019), npj Quantum Materials 5, 88 (2020)), which shows the clearest feature of DSI in solid-state systems by electrical transport experiments. To further reveal the underlying mechanism of the DSI, direct imaging of the quasi-bound states showing DSI feature in topological systems is certainly of particular importance for studying the relativistic quasi-bound states and discrete scale invariant atomic collapse in Dirac materials.
Recently, Prof. Jian Wang, Prof. X. C. Xie at Peking University, in collaboration with Prof. Minghu Pan at Shaanxi Normal University, Prof. Ping Zhang, Prof. Zi Li at Institute of Applied Physics and Computational Mathematics, Prof. Huichao Wang at Sun Yat-sen University and Prof. Haiwen Liu at Beijing Normal University, directly observed the DSI of the quasi-bound states at atomic vacancies in a topological material HfTe5. The cleaved HfTe5 surface was systematically studied by STM. On the cleaved (010) surface of HfTe5, there are a number of surface vacancies (a,c). The dI/dV spectra show a series of DOS peaks at the surface vacancies (charged impurities) with charges larger than the supercritical condition (b,d). Intriguingly, four remarkable quasi-bound states with geometric energies are observed, making the DSI feature unambiguous. dI/dV mapping measurements further reveal that the spatial distribution of these quasi-bound states is geometric too (e). The spatial distribution of quasi-bound states shows log-periodic radii (f) and the ratio between the radii is close to the energy ratio of dI/dV peaks, supporting the realization of quasi-bound states with DSI. By applying the perpendicular magnetic fields, the quasi-bound states at lower energies become wider and eventually invisible, meanwhile the energies of quasi-bound states move gradually towards the EF (g). These features are consistent with the theoretical prediction of a magnetic-field-induced transition from supercritical to subcritical states (h). The direct observation of geometric relativistic quasi-bound states sheds light on the deep understanding of the atomic collapse states, DSI and exotic quantum states in quantum Dirac materials, which would stimulate more in-depth discussions on DSI in solid state systems.
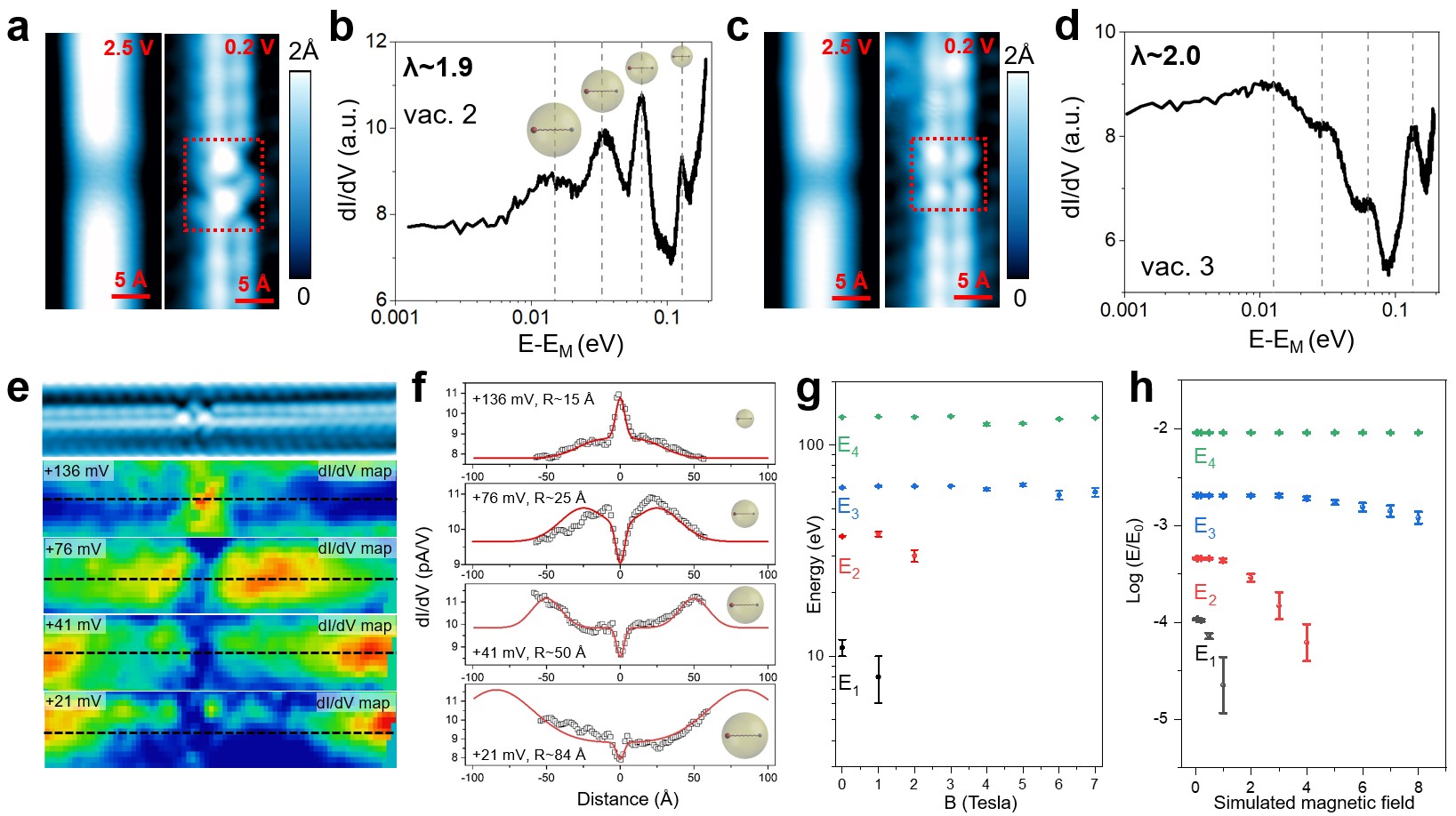
Figure: (a-d) High-resolution STM images of the HfTe5 surface vacancies (a,c) and the corresponding dI/dV spectra (b,d). Four log-periodic dI/dV peaks indicate the quasi-bound states showing discrete scale invariance at the atomic vacancies (charged impurities). (e-f) dI/dV maps taken at a series of resonance energies around the atomic vacancy (e) showing the quasi-bound states with discrete scale invariant radii (f). (g) Evolution of the energies of quasi-bound states with increasing magnetic fields. The quasi-bound states at lower energies become wider and eventually invisible, meanwhile the energies of quasi-bound states move gradually towards the EF. (h) Simulated magnetic-field-dependent energies of the quasi-bound states (normalized by the energy unit E0), which are consistent with the experimental results shown in (g).
The paper was published online by PNAS on October 10, 2022. Prof. Jian Wang at Peking University, Prof. Minghu Pan at Shaanxi Normal University and Prof. Ping Zhang at Institute of Applied Physics and Computational Mathematics are corresponding authors of this paper. Dr. Zhibin Shao at Shaanxi Normal University, Dr. Shaojian Li at Huazhong University of Science and Technology, Dr. Yanzhao Liu at Peking University and Prof. Zi Li at Institute of Applied Physics and Computational Mathematics contributed equally to this work. Other collaborators include Prof. X. C. Xie at Peking University, Prof. Huichao Wang at Sun Yat-sen University, Prof. Haiwen Liu at Beijing Normal University, Prof. Jiaqiang Yan and Prof. David Mandrus at Oak Ridge National Laboratory, etc. This work was financially supported by the National Key Research and Development Program of China, Postdoctoral Innovative Talent Support Program of China, the National Natural Science Foundation of China, Beijing Natural Science Foundation, the Strategic Priority Research Program of Chinese Academy of Sciences and China Postdoctoral Science Foundation.
Website link: https://doi.org/10.1073/pnas.2204804119
